introduction to cat qubits for dummies
second quantization
the schrodinger equation:
\[ i\hbar \frac{\partial}{\partial t}\psi(x, t) = [-\frac{\hbar^2}{2m}\nabla^2 + V(x)]\psi(x, t) \]assume we want wave function on multiple particles:
\[ \psi(x_1, x_2, x_3, ...) \]this can be linear combination of basis:
\[ \psi_i(x_1)\otimes\psi_j(x_2)\otimes\psi_k(x_3)..., i,j,k \in [1 .. \infty] \]which corresponds to
\[ \mathcal{H} = \mathcal{H_1} \otimes \mathcal{H_2} \otimes \mathcal{H_3}... \]but is this Hilbert space to large?
particles are identical items:
\[ \psi(x_1, x_2) = \pm \psi(x_1, x_2) \]fermion: electron, sign -
boson: photon, sign +
using this symmetry, we can restrict the original Hilbert space with the new basis:
\[ \psi(x_1, x_2, .., x_N) = \frac{1}{\sqrt{N!}}\sum_{\sigma \in S_N} sgn(\sigma)\psi(x_{\sigma(1)}, x_{\sigma(2)}, x_{\sigma(3)}, ..) \]the corresponding Hilbert space becomes:
\[ \mathcal{H} = \mathcal{H}^{(0)} \oplus \mathcal{H}^{(1)} \oplus \mathcal{H}^{(2)} .. \]for fermion:
\(sgn(\sigma) = +1\) if we have even number of terms in \(\sigma\), otherwise \(sgn(\sigma) = -1\)
for boson: \(sgn(\sigma) = +1\)
then we get Fock space:
\[ \psi(x_1, x_2, ..) = \sum_{n_1, n_2, ..} a_{(n_1, n_2, ..)} \ket{n_1, n_2, n_3, ..} \]and the Hamiltonian is composed of two operators:
\(\hat{a}^\dagger\): add one particle for
ith mode\(\hat{a}\): minus one particle for
ith mode
for fermion:
\[ \{ a_i, a_j^\dagger \} = a_i a_j^\dagger + a_j a_i^\dagger = \delta_{ij} \] \[ \{ a_i, a_j \} = 0 \]for boson:
\[ [ a_i, a_j^\dagger ] = a_i a_j^\dagger - a_j a_i^\dagger = \delta_{ij} \] \[ [ a_i, a_j ] = 0 \]quantum chemistry:
\[ \hat{H} = \sum_{p,q}h_{pq}\hat{a}_p^\dagger \hat{a}_q + \frac{1}{2}\sum_{p,q,r,s}h_{pqrs}\hat{a}_p^\dagger\hat{a}_q^\dagger \hat{a}_r \hat{a}_s \]quantum optics:
\[ \hat{H} = \sum_{p,q}h_{pq}\hat{a}_p^\dagger \hat{a}_q \]quantum optics
harmonic oscillator
suppose we only consider single mode:
\[ \hat{H} = \hbar \omega (\hat{n} + \frac{1}{2}) = \hbar \omega (a^\dagger a + \frac{1}{2}) \] \[ \hat{n}\ket{n} = n \ket{n} \]canonical coherent state
suppose we only consider single mode:
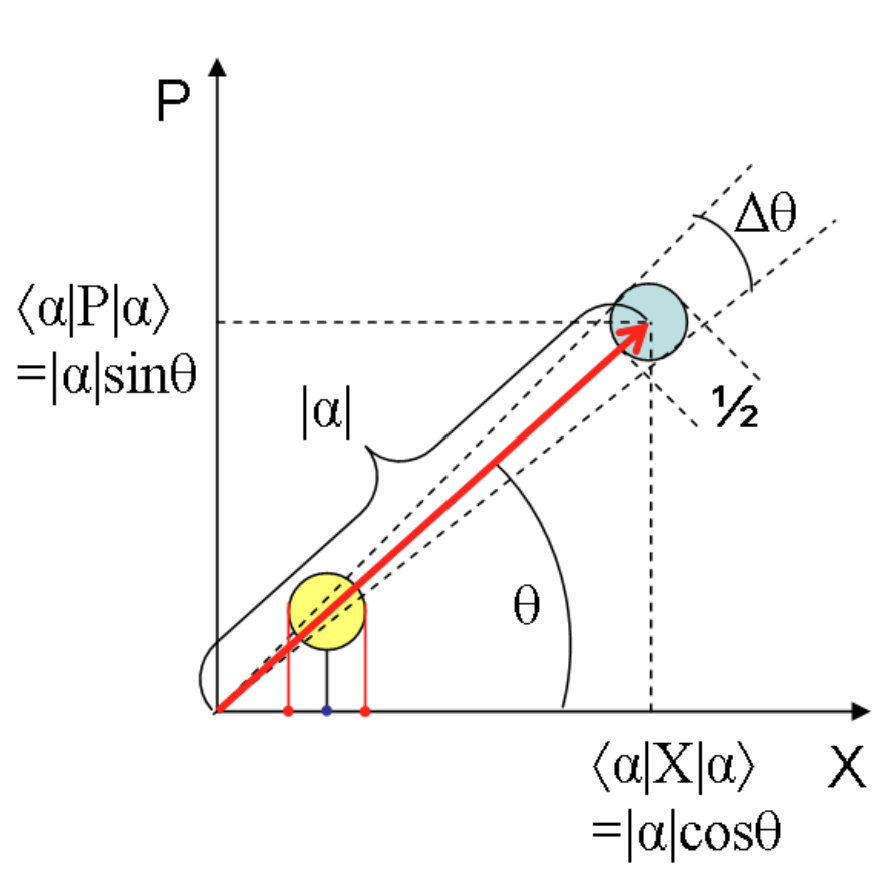
\[ \hat{a}\ket{\alpha} = \alpha\ket{\alpha} \]\(\hat{a}\) is not hermitian, \(\alpha\) in general is a complex number, i.e. \(\alpha = |\alpha|e^{i\theta}\)
\[ \ket{\alpha} = e^{-\frac{|\alpha|^2}{2}}\sum_{n=0}^{\infty}\frac{\alpha^n}{\sqrt{n!}}\ket{n} \]the photon number distribution(the probability of detecting n photons using \(\hat{n}\) operator) of coherent state follows Poissonian distribution
\[ P(n) = e^{-|\alpha|^2}\frac{\alpha^{2n}}{n!} \] \[ \braket{\hat{n}} = \bra{\alpha} \hat{n} \ket{\alpha} = |\alpha|^2 \] \[ (\Delta n)^2 = \braket{\hat{n}} - \braket{\hat{n}}^2 = |\alpha|^2 \]the photon number distribution(the probability of detecting n photons using \(\hat{n}\) operator) of coherent state follows Poissonian distribution
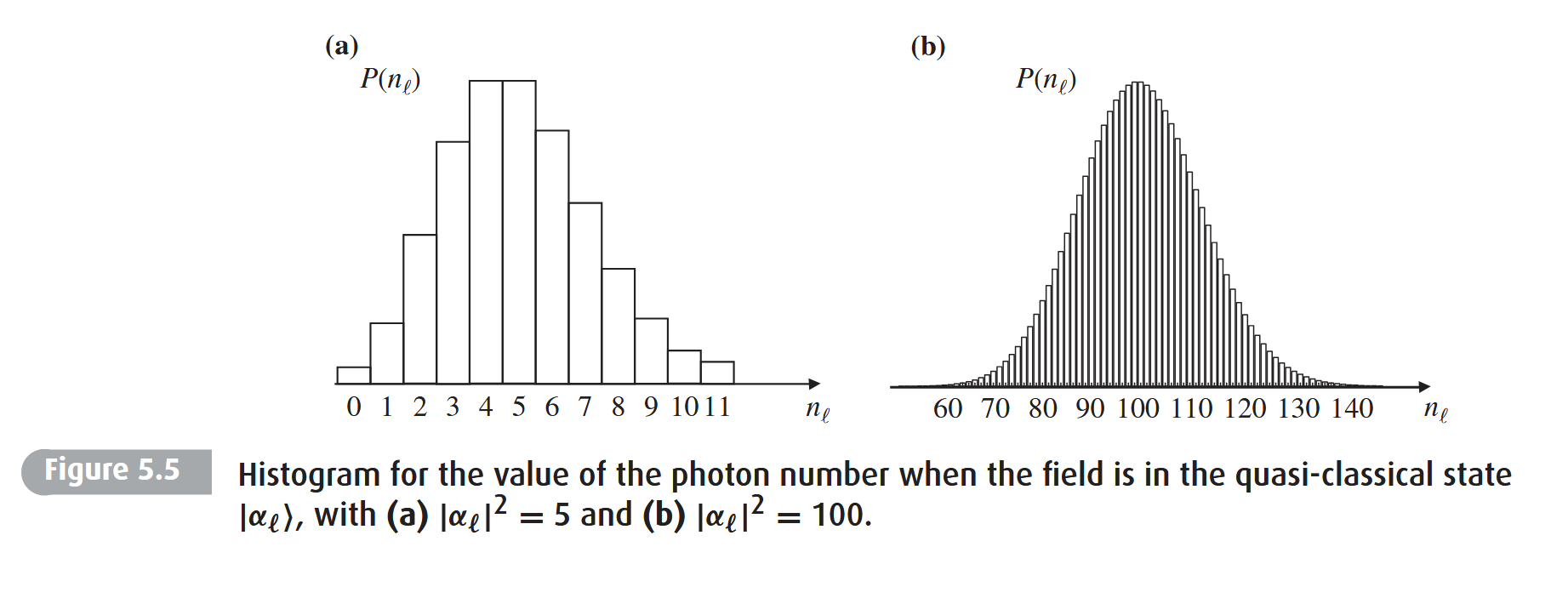
phase space plot of a coherent state
cat qubit
reference
R. Lescanne et al., “Exponential suppression of bit-flips in a qubit encoded in an oscillator,” Nat. Phys., vol. 16, no. 5, pp. 509–513, May 2020, doi: 10.1038/s41567-020-0824-x.
cat state
\[ \ket{\pm}_{\alpha} = \frac{1}{\sqrt{2(1 \pm e^{-2|\alpha|^2})}}(\ket{\alpha} \pm \ket{-\alpha}) \] \[ \ket{0}_{\alpha} = \frac{1}{\sqrt{2}}(\ket{+}_{\alpha} + \ket{-}_{\alpha}) = \ket{+\alpha} + \mathcal{O}(e^{-2|\alpha|^2}) \] \[ \ket{1}_{\alpha} = \frac{1}{\sqrt{2}}(\ket{+}_{\alpha} - \ket{-}_{\alpha}) = \ket{-\alpha} + \mathcal{O}(e^{-2|\alpha|^2}) \]All these states contain an average number of photons \(\approx |\alpha|^2\)
two photon dissipation
\[ \hat{L_2} = \sqrt{\kappa_2}(\hat{a}^2 - \alpha^2) \]two photon dissipation
Under two-photon dissipation, the cat-qubit resonator state \(\rho\) undergoes the following dynamics
\[ \frac{d}{dt}\rho = \kappa_2D[\hat{a}^2 - \alpha^2]\rho \]Lindblad operator:
\[ \forall \hat{O}, D[\hat{O}]\rho = \hat{O}\rho\hat{O}^{\dagger} - \frac{1}{2}\rho\hat{O}^{\dagger}\hat{O} - \frac{1}{2}\hat{O}^{\dagger}\hat{O}\rho \]two photon dissipation
To gain insight, we restrict this dynamics to the set of coherent states
\[ \rho(t) = \ket{\beta_t}\bra{\beta_t} \] \[ - \nabla V(\beta) = \frac{d \beta}{dt} \]two photon dissipation
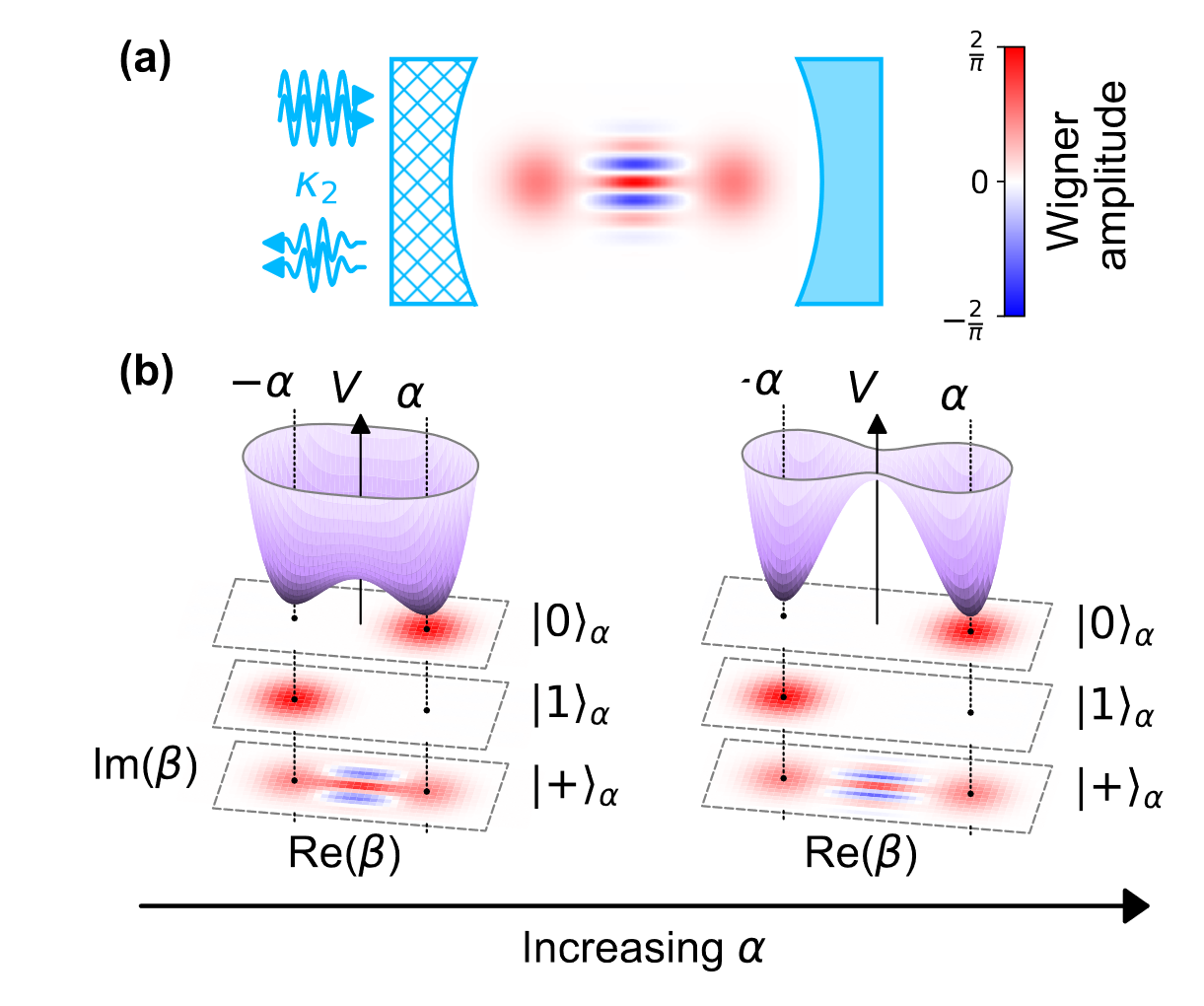
bit flip error && phase flip error
two photon dissipation
real dynamic
\[ \hat{H}_i/\hbar = g_2 (\hat{a}^\dagger)^2 \hat{b} + g_2^*\hat{a}^2\hat{b}^{\dagger} \]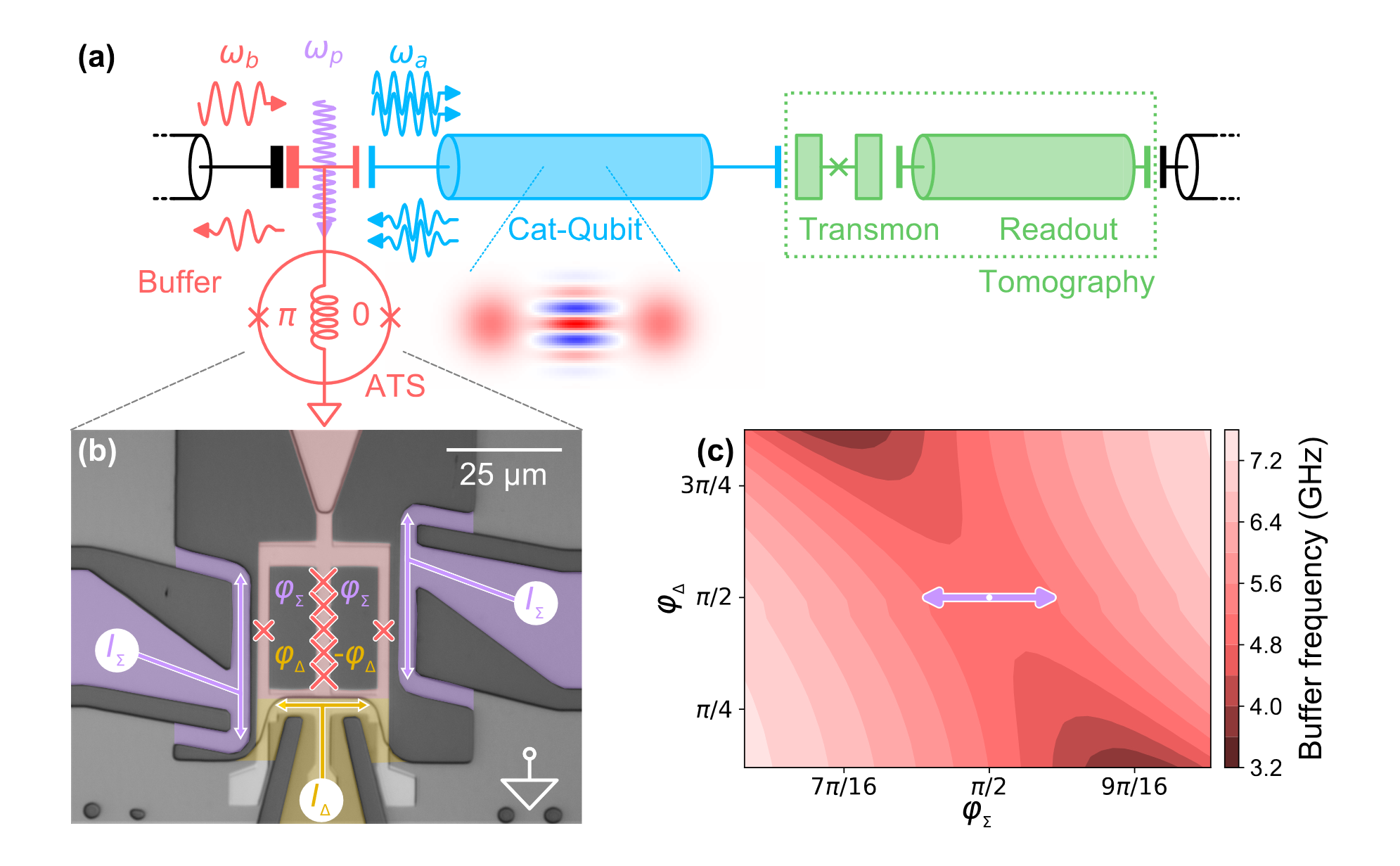
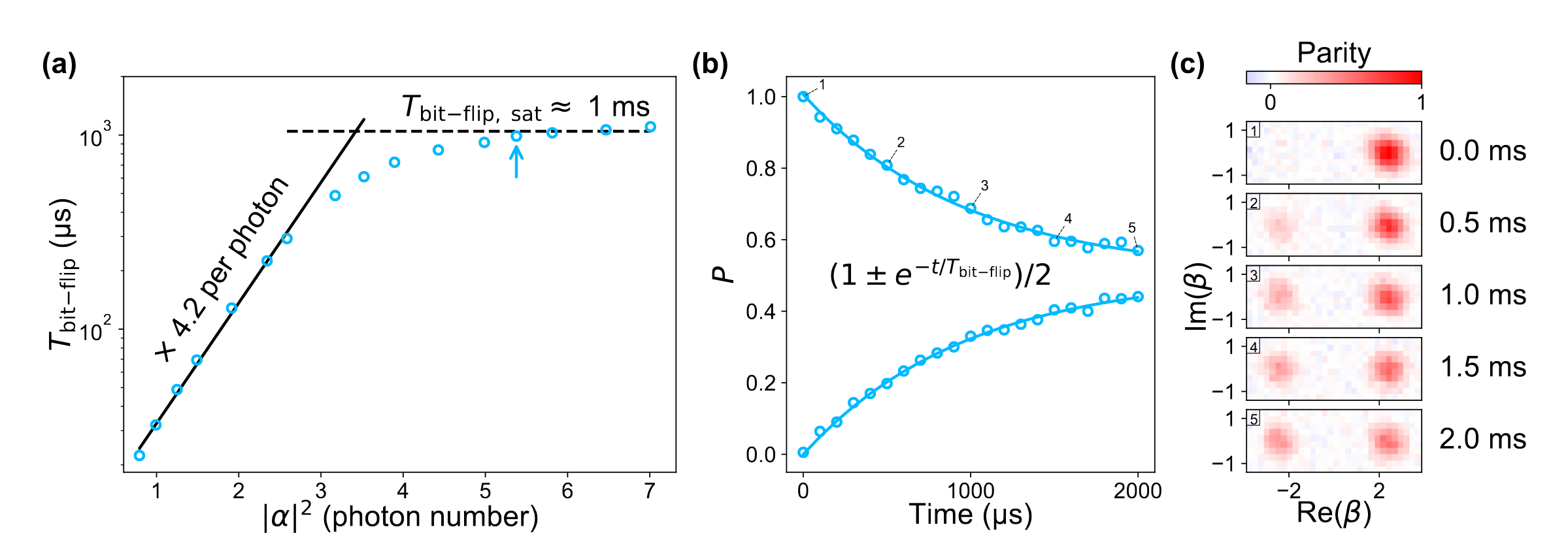
experiment - bit flip error
experiment - phase flip error
\[ \Gamma_{phase flip} = 2 |\alpha|^2 / T_{1, eff} \]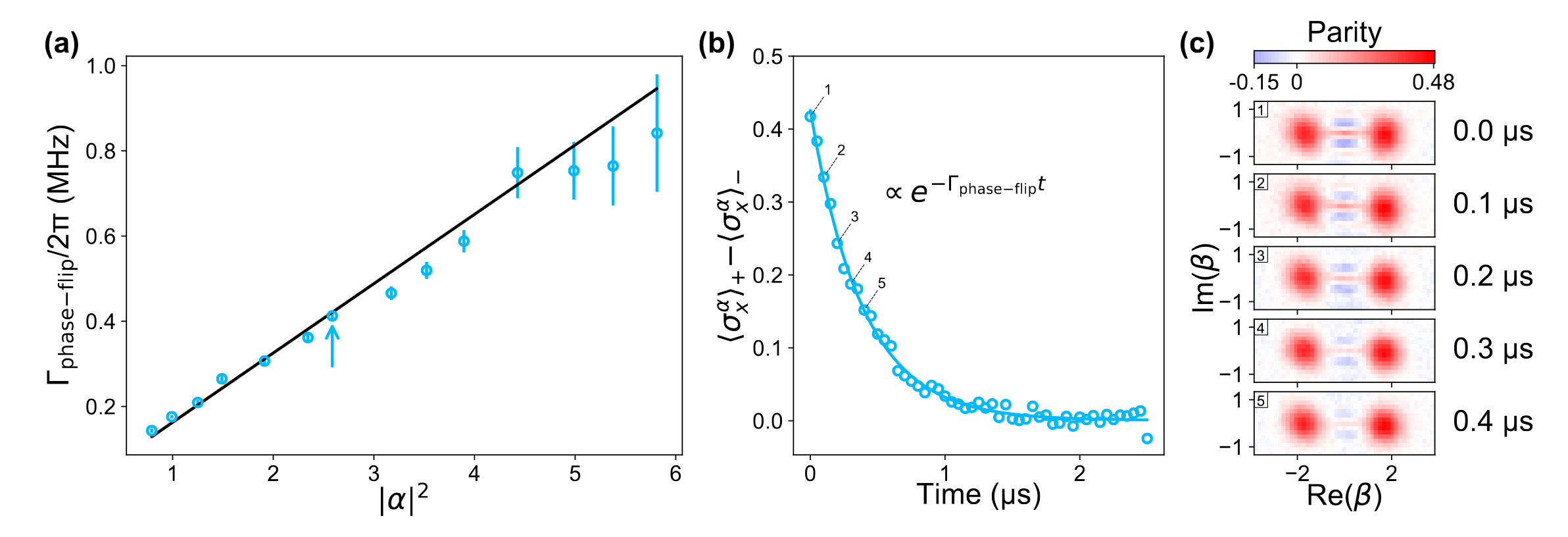
reference
[1] G. Grynberg, A. Aspect, and C. Fabre, “Introduction to Quantum Optics”.
[2] R. Lescanne et al., “Exponential suppression of bit-flips in a qubit encoded in an oscillator,” Nat. Phys., vol. 16, no. 5, pp. 509–513, May 2020, doi: 10.1038/s41567-020-0824-x.
[3] J. Guillaud, J. Cohen, and M. Mirrahimi, “Quantum computation with cat qubits,” SciPost Phys. Lect. Notes, p. 72, Jun. 2023, doi: 10.21468/SciPostPhysLectNotes.72.