theoretical background

For a quantum two-energy system, we have the following set of operations (satisfying a specific mutation relation):

\[ \hat{X}^2 = - \hat{Y}^2 = \hat{Z}^2 = \hat{I} \] \[ \hat{X}\hat{Z} = - \hat{Z}\hat{X} \] \[ [\hat{X}, \hat{Y}] := \hat{X}\hat{Y} - \hat{Y}\hat{X} = -2 \hat{Z} \] \[ [\hat{Y}, \hat{Z}] = -2\hat{X} \] \[ [\hat{Z}, \hat{X}] = 2\hat{Y} \]

This set of operations constitutes a group of Pauli operators

where we define:

\[ \hat{X}\ket{0} = \ket{1} \] \[ \hat{Z}(\ket{0} + \ket{1}) = \ket{0} - \ket{1} \]

where \(\ket{0}\), \(\ket{1}\) are the two quantum states of this two-energy system.

Computational basis versus Pauli operators

There exists a correspondence between the computational basis of a qubit and the Pauli operators we defined above, which can also be interpreted as a mutually defining relationship, namely:

We can determine a qubit's pauli operator by defining 
its computational basis, or, equivently we can determine the 
corresponding computational basis by defining the pauli operator

In the remaining part of this post, we will take advantage of this correspondence to provide the definition of a local qubit in error correction scheme.

recall: matrix representation of pauli operator

The matrix representation of the pauli operator is summarized as below:

\[ \hat{I} := \ket{0}\bra{0} + \ket{1}\bra{1} \] \[ \hat{X} := \ket{1}\bra{0} + \ket{0}\bra{1} \] \[ \hat{Y} := -i\ket{1}\bra{0} + i\ket{1}\bra{0} = \hat{X}\hat{Z} \] \[ \hat{Z} := \ket{0}\bra{0} - \ket{1}\bra{1} \]

Theoretical background-solovay-kitaev theorem

solovay-kitaev theorem is concluded as:

In order to implement an arbitrary quantum algorithm, only the following collection of gate operations is needed: \(\hat{X}\), \(\hat{Z}\), \(\hat{H}\), \(\hat{S}\), \(\hat{S}^{\dagger}\), \(\hat{T}\), \(\hat{T}^{\dagger}\), \(CNOT\)

Theoretical background - projection measurement, eigenstate and commute

The tensor representation of a Hamiltonian (which, by definition, is Hermitian) can be eigenvalue decomposed:

\[ H = U \Lambda U ^{\dagger} \]

where \(U\) is the unitary matrix and \(\Lambda\) is the diagonal matrix. It is easy to see that this decomposition is independent of the choice of coordinate system

i.e.

\[ VHV^{\dagger} = VU\Lambda U^{\dagger}V^{\dagger} \]

still holds (where \(V\) is the matrix of unitary).

\(\Lambda\) is a diagonal matrix and every value of the diagonal is non-zero (for the eigenvalues). For a qubit, we write its two eigenvalues as \(\lambda_0\), \(\lambda_1\).

\(U\) is the matrix consisting of the eigenstates in the current coordinates, i.e., the eigenstates together constitute \(\hat{U}\). For a qubit, we denote its two eigenstates as \(\ket{0}\), \(\ket{1}\). That is, \({\ket{0},\ket{1}} = \hat{U}\).

For projection measurements, with a qubit in a quantum state of \(\ket{\phi} = \alpha \ket{0} + \beta \ket{1}\), the measurer obtains, with a certain probability (\(\alpha^2\) , \(\beta^2\) ), the measurement of \(\lambda_0\) or \(\lambda_1\), and correspondingly, the system collapses into \(\ket{0}\) , \(\ket{1}\) quantum states.

Note: Here \(\ket{0}\) \(\ket{1}\) are the two eigenstates of the Hamiltonian H, which are not equivalent to the computational basis we usually talk about. For example, these two quantum states can also be written as \(\ket{+}\) \(\ket{-}\) depends on the Hamiltonian we have

Based on the basic conclusion of linear algebra, for two commuting operators, they have a common eigenstate. That is, when \(\hat{H_1}\hat{H_2} = \hat{H_2}\hat{H_1}\) , the order of measurements does not affect the quantum state at the end of these measurements.

The two operators \(\hat{X}\), \(\hat{Z}\) satisfy the definition of the Hamiltonian and can be used for projection measurements. Since \(\hat{X}\hat{Z} = -\hat{Z}\hat{X}\) does not, it is easy to see that they have no common eigenstates.

However, the two-bit operator \(\hat{X_a}\hat{X_b}\) , \(\hat{Y_a}\hat{Y_b}\) does commute:

\[ [\hat{X_a}\hat{X_b}, \hat{Y_a}\hat{Y_b}] = 0 \]

This is one of the keys to building our stabilizer.

theoretical background - stabilizer

Since the two-bit operators \(\hat{X_a}\hat{X_b}\) , \(\hat{Y_a}\hat{Y_b}\) commutes, repeated measurements using these two operators will not change the state of the system when the system is in its common eigenstate (i.e., the system is stabilized in its common eigenstate).

More generally, corresponding to multiple qubits: \({Q_0, Q_1, ... , Q_N}\) , we get a collection of operators \(\hat{X_i}\hat{X_j}, \hat{Z_k}\hat{Z_l} | i \neq j, k \neq l, |\{i,j\} \cup \{k,l\}|=2 ,or, =4\) , which are pairwise commute with each other, i.e., they have a common set of eigenstates.

Such a system can be further generalized to 4-bit operators:

\[ \hat{X_i}\hat{X_j}\hat{X_k}\hat{X_l}, \hat{Z_m}\hat{Z_n}\hat{Z_o}\hat{Z_p} | i \neq j \neq k \neq l, m\neq n \neq o \neq p, |\{i,j,k,l\} \cup \{m,n,o,p\}| = 8 ,or, = 6 \]

This set of operators still satisfies the definition of stabilizer and forms the theoretical basis of surface code.

theoretical background - stabilizer for quantum error correction

Starting with the simplest case, suppose we have a physical quantum bit in a superposition state:

\[ \ket{\phi} = \alpha \ket{0} + \beta \ket{1} \]

We additionally introduce an ancilla qubit to encode that quantum state into a higher dimensional Hilbert Space:

\[ \ket{\phi} = \alpha \ket{0} + \beta \ket{1} \to \ket{\phi}_L = \alpha \ket{00} + \beta \ket{11} = \alpha \ket{0}_L + \beta \ket{1}_L \]

Considering the operator \(Z_0Z_1\), it is easy to obtain \(\ket{\phi}_L\) as its eigenstate:

\[ Z_0Z_1\alpha \ket{00} + \beta \ket{11} = \alpha \ket{00} + \beta \ket{11} \]

recall: \(Z := \ket{0}\bra{0} - \ket{1}\bra{1}\)

This is a key point: using the above encoding, we LIFT the quantum state to a higher dimensional Hilbert Space, the quantum state then SPANS the SPACE's SUBSPACE, and all the quantum states of this subspace can be \(Z_0Z_1\) \(X_0X_1\) stabilized

continuous quantum noise

Unlike classical bits, the quantum state of a qubit is continuous, so the quantum noise acting on the qubit is also continuous. Error correction for continuous quantum noise was once thought to be impossible, but fortunately this problem was solved by the quantum error correction scheme proposed by Peter Shor in 1995. The core principle of this scheme is to discretize the continuous quantum noise randomly through measurement operations, and then correct the discrete random errors.

We first consider a simple modeling of quantum noise:

We rewrite the quantum state \(\ket{\phi}\) according to Euler's formula:

\[ \ket{\phi} = cos \frac{\theta}{2} \ket{0} + e^{i\psi}sin \frac{\theta}{2} \ket{1} \]

Then the coherence error can be modeled as follows:

\[ U(\delta \theta, \delta \psi)\ket{\phi} = cos \frac{\theta + \delta \theta}{2} \ket{0} + e^{i(\psi + \delta \psi)} sin \frac{\theta + \delta \theta}{2} \ket{1} \]

It is easy to see, that this noise can be further rewrite:

\[ U(\delta \theta, \delta \psi)\ket{\phi} = \alpha_I \mathcal{1} \ket{\phi} + \alpha_X X\ket{\phi} + \alpha_Z Z\ket{\phi} + \alpha_{XZ}XZ\ket{\phi} \]

Below we show how to discretize it

syndrom extraction

Z1Z2 syndrom

Now, let's consider the following quantum circuit:

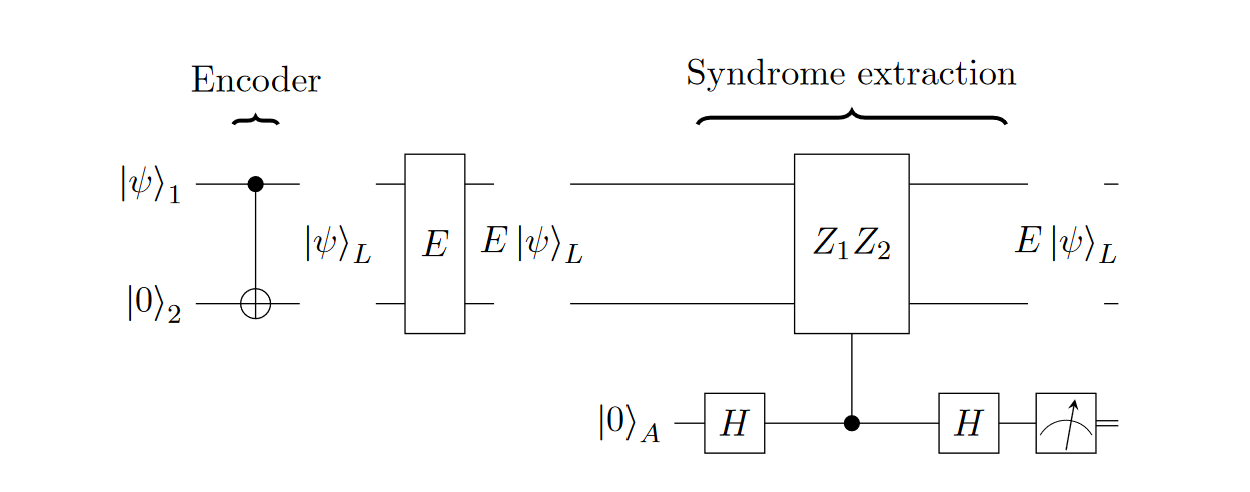
If there is no noise \(E\), it is easily obtained that measurement does not affect the quantum state \(\ket{\phi}\).

\[ \ket{A} := \hat{H}_A \ket{0}_A = \frac{\sqrt{2}}{2} \ket{0} + \frac{\sqrt{2}}{2} \ket{1} \] \[ \ket{P_1} := (Z_1Z_2)_{control}\ket{\phi}_L \otimes \ket{A} = \frac{\sqrt{2}}{2}\ket{0}\ket{\phi}_L + \frac{\sqrt{2}}{2}\ket{1} Z_1Z_2\ket{\phi}_L \] \[ \ket{P_2} := \hat{H}_A \ket{P_1} = \frac{1}{2} \ket{0} (I + Z_1Z_2)\ket{\phi}_L + \frac{1}{2}\ket{1}(I-Z_1Z_2)\ket{\phi} = \ket{0}\ket{\phi}_L \]

For simplicity, now consider only the presence of noise in qubit 0. (The qubit 1 and two-bit noise can be generalized accordingly.) Then for the above quantum circuit, our input quantum state is:

\[ \ket{\phi}_{noisy} = \alpha_I I \ket{\phi}_L + \alpha_X X_1\ket{\phi}_L + \alpha_Z Z_1\ket{\phi}_L + \alpha_{XZ}X_1Z_1\ket{\phi}_L = E\ket{\phi}_L \]

then:

\[ \bar{\ket{P_1}} := (Z_1Z_2)_{control}(I\otimes E)\ket{\phi}_L \otimes \ket{A} = \frac{\sqrt{2}}{2}(I\otimes E)\ket{0}\ket{\phi}_L + \frac{\sqrt{2}}{2} Z_1Z_2(I\otimes E)\ket{1}\ket{\phi}_L \] \[ \bar{\ket{P_2}} := \hat{H}_A \bar{\ket{P_1}} = \frac{1}{2} \ket{0} (I + Z_1Z_2)E\ket{\phi}_L + \frac{1}{2}\ket{1}(I-Z_1Z_2)E\ket{\phi}_L \]

It is easy to see that the relative phase of \(\ket{0}\ket{\phi}_L\) and \(\ket{1}\ket{\phi}_L\) changes.

recall

\[ E := \alpha_I I + \alpha_X X_1 + \alpha_Z Z_1 + \alpha_{XZ}X_1Z_1 \]

We consider this in four cases:

\(\alpha_I I\):

\[ \bar{\ket{P_2}} = \ket{0}\ket{\phi}_L = \ket{0} (\alpha \ket{00} + \beta \ket{11}) \]

\(\alpha_X X_1\):

\[ X_1\ket{\phi}_L = \alpha\ket{10} + \beta\ket{01} \] \[ Z_1Z_2X_1\ket{\phi}_L = -\alpha\ket{10} - \beta\ket{01} \] \[\bar{\ket{P_2}} = \ket{1}(\alpha\ket{10} + \beta\ket{01})\]

\(\alpha_Z Z_1\):

\[ Z_1\ket{\phi}_L = \alpha\ket{00} - \beta\ket{11} \] \[ Z_1Z_2Z_1\ket{\phi}_L = \alpha\ket{00} - \beta\ket{11} \] \[\bar{\ket{P_2}} = \ket{0}(\alpha\ket{00} - \beta \ket{11})\]

\(\alpha_{XZ}X_1Z_1\):

\[ X_1Z_1\ket{\phi}_L = \alpha\ket{10} - \beta\ket{01} \] \[ Z_1Z_2X_1Z_1\ket{\phi}_L = -\alpha\ket{10} + \beta \ket{01} \] \[\bar{\ket{P_2}} = \ket{1}(\alpha \ket{10} - \beta \ket{01})\]

Such that:

\[ \begin{aligned} \bar{\ket{P_2}} = & \\ & \alpha_I \ket{0} (\alpha \ket{00} + \beta \ket{11}) \\ & \alpha_X \ket{1}(\alpha\ket{10} + \beta\ket{01}) \\ & \alpha_Z \ket{0}(\alpha\ket{00} - \beta \ket{11}) \\ & \alpha_{XZ} \ket{1}(\alpha \ket{10} - \beta \ket{01}) \end{aligned} \]

It can be noticed that after a measurement

The system is

• either at \(\alpha_I (\alpha \ket{00} + \beta \ket{11}) + \alpha_Z (\alpha \ket{00} - \beta \ket{11})\)

• or at \(\alpha_X(\alpha\ket{10} + \beta\ket{01}) + \alpha_{XZ}(\alpha\ket{10} - \beta\ket{01})\).

If we restrict the type of noise to X noise of arbitrary amplitude( i.e. \(\alpha_Z\) and \(\alpha_{XZ}\) terms do not exists), we see that

The system is

• either in \(\alpha\ket{00} + \beta \ket{11}\)

• or at \(\alpha\ket{10} + \beta \ket{01}\)

At this point the continuous noise is discretized: \(\alpha_X\) no longer exists!

As can be seen, the above encoding is not very practically useful: it cannot handle arbitrary single-bit noise, thus it can only serve as a simple demonstration of the idea that discretization through measurement is feasible.

For better protection of quantum states, we need more complete coding methods, such as surface code. An thoroughly introduction to the surface code may remain for future posts.

Reference:

[1] J. Roffe, “Quantum Error Correction: An Introductory Guide,” Jul. 25, 2019. doi: 10.1080/00107514.2019.1667078.